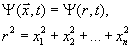Όταν το ελατήριο έχει μάζα. (Massive spring)

         

         Υποθέτουμε ότι το ελατήριο του παραπάνω σχήματος έχει μάζα m και σταθερά k και ενώ το αριστερό άκρο του συνδέεται σε σταθερό σημείο, στο δεξιό άκρο υπάρχει δεμένο σώμα μάζας Μ. Ποια είναι η περίοδος των ταλαντώσεων, αν εκτρέψουμε από τη θέση ισορροπίας το σύστημα και το αφήσουμε να ταλαντωθεί;

Όταν το ελατήριο έχει μάζα.

Για τις προσεγγίσεις στη Φυσική.

               
            " Είναι χαρακτηριστικό του εκπαιδευμένου πνεύματος το ότι μένει ικανοποιημένο με το βαθμό ακρίβειας που επιτρέπει η φύση του ζητήματος και δεν αναζητεί την απόλυτη ακρίβεια εκεί όπου είναι δυνατή μόνο η προσέγγιση της αλήθειας"...
                                                                                       
                                                                                                                      ΑΡΙΣΤΟΤΕΛΗΣ





         Το να μπορεί κανείς να κάνει τις σωστές προσεγγίσεις σε διάφορα προβλήματα Φυσικής (και όχι μόνο) είναι σίγουρα μια πολύ σημαντική ικανότητα. Κι΄ όμως στα περισσότερα (αν όχι όλα) σχολικά ή και Πανεπιστημιακά βιβλία δεν δίνεται (κατά τη γνώμη μου) ιδιαίτερη έμφαση στην «καλλιέργεια» αυτής της ικανότητας. Ούτε και υπάρχει κάποια συστηματική παρουσίαση του τρόπου με τον οποίο θα μπορούσε –ίσως- κάποιος να «εξασκηθεί» στο να επιλέγει την καλύτερη (ανάλογα με το πρόβλημα) δυνατή προσέγγιση.


(Ακολουθεί μια μικρή εργασία για τις προσεγγίσεις): 

Λίγα για τις προσεγγίσεις

                          
                            http://img.tfd.com/wiki/8/81/Approximation_volume_deformation.png

Εργαστήριο πυκνότητας (μετάλλων). Density Lab (metals - Easy Java Simulation)

http://www.stevespanglerscience.com/img/cache/bcb9b8db117ee64376aedaf7af3595ca/sevenlayer-2-51908.jpg

         Το φυσικό μέγεθος πυκνότητα αποτελεί βασικό χαρακτηριστικό της ύλης και συμβολίζεται με το
γράμμα ρ (ή και με το d, από τη λέξη density = πυκνότητα). Η πυκνότητα ενός σώματος ορίζεται ως το πηλίκο της μάζας του δια του όγκου του:

Έτσι λοιπόν η πυκνότητα εκφράζει τη μάζα ανά μονάδα όγκου του θεωρούμενου υλικού.

Μονάδα μέτρησης της πυκνότητας στο Διεθνές Σύστημα Μονάδων είναι το 1 kg/m³. Αρκετά συχνά όμως σαν μονάδα χρησιμοποιείται και το γραμμάριο ανά κυβικό εκατοστό, 1 g/cm³.
 
        Η πυκνότητα των υγρών σωμάτων μεταβάλλεται πολύ λίγο για μεγάλες μεταβολές πίεσης και θερμοκρασίας και γι’ αυτό μπορούμε να την θεωρούμε πρακτικά σταθερή. Όσον αφορά τα αέρια σώματα, η πυκνότητα τους μεταβάλλεται εύκολα, όταν μεταβάλλεται η πίεση ή/και η θερμοκρασία.


               Πυκνότητα - Βικιπαίδεια

ΠΥΚΝΟΤΗΤΕΣ ΔΙΑΦΟΡΩΝ ΥΛΙΚΩΝ
Υλικό	Πυκνότητα (kg/m3)
αέρας (στους 20 οC)	1,2
αέρας (στους 0 οC)	1,3
φελλός	250
οινόπνευμα	800
ελαιόλαδο	900
πάγος	920
νερό	1000
τσιμέντο	2400
αλουμίνιο	2700
σίδηρος	7800
μόλυβδος	11340
υδράργυρος	13600
χρυσός	19300
όσμιο	22587

       Για ένα "εικονικό εργαστήριο" πυκνότητας των μετάλλων:

Πηγαίνουμε στην ιστοσελίδα του (φίλου και συνάδελφου) Θανάση Γεράγγελου:

http://users.sch.gr/ageragge/ejsSims/ejsSims.htm

Βρίσκουμε το αρχείο (EJS, Easy Java Simulation):

ejs_Density_Lab.jar,

το οποίο με δεξί κλικ αποθηκεύουμε, ώστε να μπορούμε να το "τρέξουμε" όποτε επιθυμούμε.

Κατόπιν, κατεβάζουμε το φύλλο εργασίας:


Εργαστήριο πυκνότητας μετάλλων,


και (ακολουθώντας τις οδηγίες) συμπληρώνουμε τις ερωτήσεις, ώστε να οδηγηθούμε τελικά σε κάποια συμπεράσματα για το φυσικό μέγεθος που ονομάζουμε πυκνότητα.

Η ΙΣΤΟΡΙΑ ΤΟΥ π ΤΕΤΑΡΤΟ ΜΕΡΟΣ

         Στην Ευκλείδεια Γεωμετρία, η μαθηματική σταθερά π είναι ένας πραγματικός αριθμός που μπορεί να οριστεί ως ο λόγος του μήκους της περιφέρειας ενός κύκλου προς τη διάμετρό του. Ο αριθμός αυτός χρησιμοποιείται πολύ συχνά στα μαθηματικά, τη φυσική και τη μηχανολογία. Ο συμβολισμός προέρχεται από το αρχικό γράμμα «π» (πι) της λέξης «περιφέρεια», και έχει καθιερωθεί διεθνώς, ενώ στο λατινικό αλφάβητο συμβολίζεται ως Pi, όταν δεν είναι διαθέσιμοι τυπογραφικά ελληνικοί χαρακτήρες. ( Ο Ουαλός μαθηματικός William Jones ήταν ο πρώτος που χρησιμοποίησε το σύμβολο «π» στα 1706, ενώ στη μαθηματική βιβλιογραφία καθιερώθηκε από τον διάσημο Ελβετό μαθηματικό Leonhard Euler στα 1737). Το π είναι γνωστό επίσης ως σταθερά του Αρχιμήδη .

                                                                            Αρχιμήδης

Η Ιστορία του π, μέρος IV

Επίσης:


Η Ιστορία του π, μέρος ΙΙΙ 

Η Ιστορία του π, μέρος ΙΙ 

Η Ιστορία του π, μέρος I

Ελατήριο ανάμεσα σε δύο μάζες. "Ανηγμένη" μάζα.

         Στο παρακάτω σχήμα, στα άκρα Α και Β ελατηρίου με σταθερά k, είναι στερεωμένα δύο σώματα με μάζες m₁ και m₂ , αντίστοιχα. Το ελατήριο θεωρείται χωρίς μάζα ενώ το σύστημα μάζες-ελατήριο μπορεί να ταλαντώνεται ελεύθερα (χωρίς τριβές) στο λείο οριζόντιο επίπεδο, στο οποίο στηρίζεται.  Αρχικά τεντώνουμε το ελατήριο και στη συνέχεια το αφήνουμε ελεύθερο. Να περιγραφεί η ταλάντωση του συστήματος.

 

ΕΛΑΤΗΡΙΟ ΑΝΑΜΕΣΑ ΣΕ ΔΥΟ ΜΑΖΕΣ. ΑΝΗΓΜΕΝΗ ΜΑΖΑ

Προσωπική σελίδα Θανάση Γεράγγελου

          Μία ιστοσελίδα που πραγματικά αξίζει τον κόπο να επισκεφθεί κανείς είναι αυτή του καλού συνάδελφου και φίλου από τα φοιτητικά ήδη χρόνια στα τέλη της δεκαετίας του '70 και στις αρχές αυτής του '80, Θανάση Γεράγγελου. Για πολλούς συνάδελφους στο Περιστέρι ο Θανάσης είναι γνωστός ως ο "Δάσκαλος". Και αυτό δεν είναι τυχαίο. Υπήρξε ήδη πολύ καλός δάσκαλος-καθοδηγητής  για πολλούς από εμάς όταν ήμασταν φοιτητές, όντας λίγο μεγαλύτερος και όντας πάντοτε πρόθυμος να προσφέρει τις γνώσεις του. Αργότερα υπήρξε και επιμορφωτής για αρκετούς από εμάς στις νέες τεχνολογίες και ειδικότερα στα λογισμικά Modellus και Interactive Physics. Ο Θανάσης τον τελευταίο καιρό ασχολείται με προσομοιώσεις EJS (Easy Java Simulations), με εξαιρετική, όπως εύκολα μπορεί να διαπιστώσει κανείς βλέποντας τη δουλειά του, επιτυχία...

Προσωπική σελίδα Θανάση Γεράγγελου

Προσομοιώσεις Φυσικής

Ηλεκτρομαγνητική θεωρία στις n+1 διαστάσεις. Νόμος του Gauss.

        Θεωρούμε ηλεκτρομαγνητική θεωρία σε n+1διαστάσεις (n χωρικές και 1 χρονική), η οποία περιγράφεται από τη Λαγκρανζιανή:

                                                                             

Θα επιχειρήσουμε να βρούμε τον αντίστοιχο νόμο του Gauss για το ηλεκτρικό πεδίο και να υπολογίσουμε το ηλεκτροστατικό δυναμικό ενός σημειακού ηλεκτρικού φορτίου σε η χωρικές διαστάσεις.

       Στη συνέχεια θα δείξουμε ότι αν τα ηλεκτρόνια κινούνται σε δυναμικό:

                   

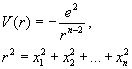
Στις η-χωρικές διαστάσεις, για να σχηματισθούν σταθερά άτομα πρέπει να είναι: n=3. Δηλαδή μόνον σε 3 χωρικές διαστάσεις μπορούν να υπάρξουν σταθερά άτομα (και κατά συνέπεια Χημεία, Βιολογία, και τελικά...εμείς)....

Carl Friedrich Gauss

ΗΛΕΚΤΡΟΜΑΓΝΗΤΙΚΗ ΘΕΩΡΙΑ ΣΕ n ΧΩΡΙΚΕΣ ΔΙΑΣΤΑΣΕΙΣ

(Ευχαριστώ πολύ το συνάδελφο Σινάνη Χρήστο για τις συζητήσεις που είχαμε πάνω στο συγκεκριμένο θέμα)

Υπερσυμμετρικές μέθοδοι σε προβλήματα Κβαντικής Μηχανικής (I)

             Στο πρώτο μέρος της εργασίας, με τίτλο Υπερσυμμετρικές μέθοδοι σε προβλήματα Κβαντικής Μηχανικής (I),  που μπορείτε να βρείτε στον σύνδεσμο που ακολουθεί,  θα δούμε  μια πολύ συνοπτική περιγραφή-επανάληψη της μη σχετικιστικής κβαντομηχανικής σε μία διάσταση (απλός αρμονικός ταλαντωτής με την βοήθεια  των τελεστών ανόδου και καθόδου).  Στη συνέχεια θα δούμε  την έννοια του  υπερδυναμικού  (superpotential) και  τα λεγόμενα δυναμικά  συνοδείας,  που μας εισάγουν στις έννοιες  και τις μεθόδους της υπερσυμμετρικής  κβαντομηχανικής.

             Θα αναφερθούμε   στην έννοια   της  «σπασμένης  ή  –μη--  υπερσυμμετρίας»  (broken or unbroken supersymmetry)  και  στον δείκτη του  Witten  μέσω   του οποίου προσδιορίζουμε αν έχουμε περίπτωση σπασμένης  ή  μη υπερσυμμετρίας. Θα ορίσουμε την  «υπερσυμμετρική Χαμιλτονιανή»  και  τους  τελεστές υπερφορτίου  και  πως εφαρμόζονται  ειδικότερα   στην  περίπτωση  του  αρμονικού  ταλαντωτή.  Θα δούμε τον τρόπο με  τον οποίο «κατασκευάζουμε» μια  «ιεραρχία»  Χαμιλτονιανών, και πως  "αντιμετωπίζουμε"  το πρόβλημα της σκέδασης με τη βοήθεια της  υπερσυμμετρίας.  

(Η ανάρτηση αυτή αφιερώνεται στο Δημήτρη Μυρογιάννη).

Υπερσυμμετρικές μέθοδοι σε προβλήματα Κβαντικής Μηχανικής (I)

         

ΕΥΧΑΡΙΣΤΙΕΣ

         

     Ένα μεγάλο ΕΥΧΑΡΙΣΤΩ στο συνάδελφο και φίλο Δημήτρη Μυρογιάννη, ο οποίος βοήθησε στο να "ελαφρύνει" σημαντικά το ιστολόγιο γράφοντας τον κώδικα για την δυνατότητα ενεργοποίησης ή μη (κατόπιν επιλογής) κάποιων gadgets.

Η ΕΞΙΣΩΣΗ ΤΟΥ ΚΥΜΑΤΟΣ ΣΤΙΣ n+1 ΔΙΑΣΤΑΣΕΙΣ

              Στα επόμενα θα προσπαθήσουμε να λύσουμε την εξίσωση του κύματος (1) σε n+1 διαστάσεις:

                                                                                          

για σφαιρικά συμμετρικό κύμα:

                                                                                 

και θα προσπαθήσουμε να δούμε (σε επίπεδο λύσεων), ότι η αρχή του Huygens ισχύει μόνο για περιττές χωρικές διαστάσεις: ν=1,3,5,...

         Η ΕΞΙΣΩΣΗ ΤΟΥ ΚΥΜΑΤΟΣ ΣΤΙΣ n+1 ΔΙΑΣΤΑΣΕΙΣ