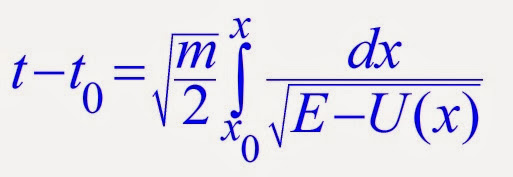Ολοκλήρωση των εξισώσεων κίνησης (III). Μια ενδιαφέρουσα περίπτωση.

           Σαν ένα τρίτο παράδειγμα ολοκλήρωσης των εξισώσεων κίνησης, μελετάμε μια περίπτωση που παρουσιάζει ενδιαφέρον...

Ολοκλήρωση των εξισώσεων κίνησης (III). Μια ενδιαφέρουσα περίπτωση.   (Dropbox)

                                                                    ή επίσης:

Ολοκλήρωση των εξισώσεων κίνησης (III). Μια ενδιαφέρουσα περίπτωση.    (Scribd)


                                  

Ολοκλήρωση των εξισώσεων κίνησης (II). Η περίπτωση του αρμονικού ταλαντωτή.

Σαν ένα δεύτερο παράδειγμα ολοκλήρωσης των εξισώσεων κίνησης, μελετάμε το δυναμικό του αρμονικού ταλαντωτή...

Ολοκλήρωση των εξισώσεων κίνησης (II). Η περίπτωση του αρμονικού ταλαντωτή.     (Dropbox)

                                                          ή επίσης:

Ολοκλήρωση των εξισώσεων κίνησης (II). Η περίπτωση του αρμονικού ταλαντωτή.     (Scribd)

  

http://en.citizendium.org/wiki/File:Harmonic_field.png

Ολοκλήρωση των εξισώσεων κίνησης (I). Η απλή περίπτωση της σταθερής δύναμης.

      Στην εργασία που ακολουθεί, βρίσκουμε το (πρώτο) ολοκλήρωμα της κίνησης για την απλή περίπτωση της σταθερής δύναμης:

Ολοκλήρωση των εξισώσεων κίνησης (I). Η απλή περίπτωση της σταθερής δύναμης. (Dropbox)

                                                                           ή επίσης:

Ολοκλήρωση των εξισώσεων κίνησης (I). Η απλή περίπτωση της σταθερής δύναμης.  (Scribd)

Μετασχηματισμοί βαθμίδας (στον ηλεκτρομαγνητισμό).

    Στον παρακάτω σύνδεσμο, υπάρχει μια μικρή αναφορά στους μετασχηματισμούς βαθμίδας (ειδικότερα στον ηλεκτρομαγνητισμό):

Μετασχηματισμοί βαθμίδας (στον ηλεκτρομαγνητισμό).

 

Ταλαντώσεις σώματος αλλά και συστήματος ή περί ανηγμένης μάζας και άλλα σχετικά.(Του Διονύση Μάργαρη).

     Τα  δυο σώματα Α και Β με ίσες μάζες m₁=m₂=m=1kg, ηρεμούν όπως στο σχήμα, όπου το ελατήριο έχει σταθερά k=100Ν/m, ενώ το Α βρίσκεται σε ύψος h=0,2m από το έδαφος. Απομακρύνουμε κατακόρυφα προς τα πάνω το σώμα Α, κατά y₁=0,1m και σε μια στιγμή που θεωρούμε t=0, το αφήνουμε ελεύθερο να κινηθεί εκτελώντας ΑΑΤ.

i) Να βρεθεί η εξίσωση της απομάκρυνσής του σε συνάρτηση με το χρόνο, θεωρώντας την προς τα πάνω κατεύθυνση θετική.

ii) Να βρεθεί η εξίσωση της τάσης του νήματος σε συνάρτηση με το χρόνο και να γίνει η γραφική της παράσταση.

iii) Τη στιγμή που η τάση του νήματος γίνεται ελάχιστη για τρίτη φορά, το νήμα κόβεται και τα σώματα πέφτουν. Με την κρούση με το έδαφος το σώμα Α προσκολλάται. Να βρεθεί η ενέργεια της ταλάντωσης που θα εκτελέσει το Β σώμα.

Δίνεται g=10m/s².

 

Ταλαντώσεις σώματος αλλά και συστήματος ή περί ανηγμένης μάζας και άλλα σχετικά.

(Η εργασία έχει αναρτηθεί στο δίκτυο "Υλικό Φυσικής Χημείας" του φίλου και  συνάδελφου Διονύση Μάργαρη.)

ΜΗΔΕΝΙΚΟΣ ΣΤΡΟΒΙΛΙΣΜΟΣ ΚΑΙ ΣΥΝΤΗΡΗΤΙΚΟ ΠΕΔΙΟ.

      Ένα πεδίο δυνάμεων χαρακτηρίζεται συντηρητικό, όταν το έργο (επικαμπύλιο ολοκλήρωμα) της δύναμης σε οποιαδήποτε διαδρομή είναι ανεξάρτητο της ακολουθούμενης διαδρομής και εξαρτάται μόνο από την αρχή και το τέλος (άκρα της διαδρομής). Σε ένα τέτοιο πεδίο, το έργο κατά μήκος οποιασδήποτε κλειστής διαδρομής (κλειστό επικαμπύλιο ολοκλήρωμα) είναι ίσο με το μηδέν.

      Όταν ένα πεδίο δυνάμεων είναι συντηρητικό, τότε ο στροβιλισμός της δύναμης είναι ίσος με το μηδέν. Αυτό προκύπτει από το θεώρημα του Stokes (ή του Green, αν είμαστε στο επίπεδο). Το ερώτημα είναι: Αν γνωρίζουμε ότι ο στροβιλισμός της δύναμης είναι μηδέν, μπορούμε να πούμε (με βεβαιότητα) ότι το πεδίο είναι συντηρητικό;   

     Θα προσπαθήσουμε να απαντήσουμε στο ερώτημα με τη βοήθεια ενός παραδείγματος:      

ΜΗΔΕΝΙΚΟΣ ΣΤΡΟΒΙΛΙΣΜΟΣ ΚΑΙ ΣΥΝΤΗΡΗΤΙΚΟ ΠΕΔΙΟ. 

                                     Sir George Gabriel Stokes

Και μια "κωδικοποίηση":

ΟΛΟΚΛΗΡΩΜΑ ΑΝΕΞΑΡΤΗΤΟ ΤΗΣ ΤΡΟΧΙΑΣ

Λίγα για την ακτινοβολία Hawking (Hawking radiation).

  

       Πρόκειται για ακτινοβολία που εκπέμπεται από μια μαύρη τρύπα και είναι αποτέλεσμα κβαντομηχανικών διεργασιών. Θεωρητικά επιχειρήματα για την ύπαρξη και την προέλευσή της, έδωσε για πρώτη φορά στα 1974 ο Stephen Hawking. Το ισχυρό βαρυτικό πεδίο της μαύρης τρύπας, κοντά στην περιοχή του ορίζοντα γεγονότων, προκαλεί τη δημιουργία ζεύγους σωματιδίου-αντισωματιδίου. Ένα μέλος του  κάθε ζεύγους (το σωματίδιο ή το αντισωματίδιο) «πέφτει» μέσα στη μαύρη τρύπα, ενώ το άλλο διαφεύγει. Έτσι για έναν εξωτερικό παρατηρητή, η μαύρη τρύπα φαίνεται ότι εκπέμπει ακτινοβολία (ακτινοβολία Hawking)...

 Λίγα για την ακτινοβολία Hawking (Hawking radiation).

Λίγα για την κοσμική ακτινοβολία υποβάθρου.

      Το Σύμπαν διαστέλλεται και ψύχεται. Στα αρχικά στάδια αυτής της διαστολής, η θερμοκρασία ήταν τόσο πολύ υψηλή ώστε η ενεργειακή πυκνότητα της ακτινοβολίας ήταν τόσο μεγάλη που απέτρεπε τον σχηματισμό ατόμων ( kT >>1eV , όπου k είναι η σταθερά Boltzmann και T η απόλυτη θερμοκρασία). Την περίοδο αυτή η ακτινοβολία ήταν συζευγμένη με τα ελεύθερα ηλεκτρόνια , και τα πρωτόνια με τα οποία παρέμενε σε θερμική ισορροπία…

Λίγα για την κοσμική ακτινοβολία υποβάθρου. 

Επίλυση της κυματικής εξίσωσης και εφαρμογές. (Του Ευάγγελου Κορφιάτη, Phd)

     Στην εργασία του αυτή ο φίλος και συνάδελφος Ευάγγελος Κορφιάτης (Phd), επιλύει την κυματική εξίσωση δίνοντας παράλληλα πολλά παραδείγματα και εφαρμογές:


Επίλυση της κυματικής εξίσωσης και εφαρμογές. (Του Ευάγγελου Κορφιάτη, Phd).


 (Η εργασία έχει αναρτηθεί στο δίκτυο "Υλικό Φυσικής Χημείας" του φίλου και  συνάδελφου Διονύση Μάργαρη.)
http://ylikonet.gr/profiles/blogs/3647795:BlogPost:68582






                                                    Jean-Baptiste le Rond d'Alembert

 

Augustin-Louis Cauchy

ΣΧΕΤΙΚΙΣΤΙΚΗ ΚΙΝΗΜΑΤΙΚΗ ΓΙΑ ΣΤΑΘΕΡΗ ΔΥΝΑΜΗ

      Ας θεωρήσουμε την απλούστερη δυνατή περίπτωση δηλαδή τη μονοδιάστατη περίπτωση κατά την οποία μια σταθερή δύναμη δρα πάνω σε ένα αρχικά ακίνητο σώμα μάζας m. Ας υποθέσουμε λοιπόν ότι η δύναμη αυτή επιδρά στο σώμα για χρόνο t και ότι το σώμα αποκτά ταχύτητα υ(t). Θα έχουμε:...

 ΣΧΕΤΙΚΙΣΤΙΚΗ ΚΙΝΗΜΑΤΙΚΗ ΓΙΑ ΣΤΑΘΕΡΗ ΔΥΝΑΜΗ