(Ευχαριστώ το συνάδελφο Γιάννη Καλατζή για την ορθογραφική και συντακτική διόρθωση στον τίτλο της ανάρτησης)
Johan Bernoulli
http://www.librosmaravillosos.com/matematicalife/imagenes/113a.gif
http://online.redwoods.cc.ca.us/instruct/darnold/calcproj/fall98/nateb/iv14m.gif
According to Fermat’s principle: The actual path between two points taken by a beam of light is the one which is traversed in the least time. Johann Bernoulli used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).[1]
The conservation law can be used to express the speed of a body in a constant gravitational field as:
Johann Bernoulli noted that the law of refraction gives a constant of the motion for a beam of light in a medium of variable density:
The equations above allow us to draw two conclusions:
Johann's brother Jakob showed how 2nd differentials can be used to obtain the condition for least time. A modernized version of the proof is as follows. If we make a negligible deviation from the path of least time then, for the differential triangle formed by the displacement along the path and the horizontal and vertical displacements,
http://curvebank.calstatela.edu/brach3/brach3.htm
Η (χειρόγραφη) λύση του Newton:
http://www.cosmeo.com/images/pictures/player/BE063184.jpg
Στον παρακάτω σύνδεσμο έχω μια μικρή εργασία για το πως,εφαρμόζοντας τις μεθόδους του λογισμού των μεταβολών(Euler-Lagrange) μπορούμε να αποδείξουμε ότι η συντομότερη γραμμή που συνδέει δύο σημεία (στον Ευκλείδιο χώρο) είναι η ευθεία που περνάει από τα σημεία αυτά.
ΕΥΘΕΙΑ
Και μια πολύ ωραία προσομοίωση για τη βραχιστόχρονη καμπύλη, μέσω του scratch , από το συνάδελφο Νίκο Δαπόντε:
Τέλος ένα πολύ ενδιαφέρον Site για τη βραχιστόχρονη καμπύλη:
http://curvebank.calstatela.edu/brach/brach.htm
http://curvebank.calstatela.edu/brach2/cucloid2.jpg
http://t2.gstatic.com /images?q=tbn:ANd9GcTnI6ykpUcSVloODQYolsdLUHQwV7oVEk6Roc62C82zaFPIQ6-2
Johan Bernoulli
http://www.librosmaravillosos.com/matematicalife/imagenes/113a.gif
http://online.redwoods.cc.ca.us/instruct/darnold/calcproj/fall98/nateb/iv14m.gif
Ο Johann Bernoulli έθεσε το πρόβλημα της βραχιστόχρονης (brachistochrone) καμπύλης προς τους αναγνώστες του Acta Eruditorum τον Ιούνιο, 1696. Δημοσίευσε τη λύση του στο περιοδικό τον Μάιο του επόμενου έτους, και υπογράμμισε ότι η λύση είναι η ίδια καμπύλη με την ταυτόχρονη ( tautochrone) καμπύλη του Huygens . Πέντε μαθηματικοί απάντησαν με λύσεις: ο Ισαάκ Νεύτων , ο Jakob Bernoulli (αδελφός του Johann), ο Gottfried Leibniz , ο Ehrenfried Walther von Tschirnhaus και ο Guillaume de l'Hopital . Τέσσερις από τις λύσεις (εκτός αυτής του de l'Hôpital) δημοσιεύθηκαν στην ίδια έκδοση του περιοδικού, μαζί με αυτή του Johann Bernoulli .
Σε μια προσπάθεια να ξεπεράσει τον αδελφό του, Jacob Bernoulli ο Johan δημιούργησε μια σκληρότερη εκδοχή του brachistochrone προβλήματος. Στην προσπάθεια επίλυσής του, ανέπτυξε νέες μεθόδους που τελειοποιήθηκαν αργότερα από τον Λέοναρντ Όιλερ σε αυτό που ονομάζουμε λογισμό των μεταβολών .Ο Joseph-Louis de Lagrange συνέχισε τις έρευνες που τελικά οδήγησαν σε μια σύγχρονη εκδοχή του απειροστικού λογισμού .
Ο Γαλιλαίος επιχείρησε να λύσει ένα παρόμοιο πρόβλημα για την πορεία της ταχύτερης καθόδου από ένα σημείο σε ένα τοίχο στο έργο του δύο νέες επιστήμες το 1638. Κατέληξε στο συμπέρασμα ότι το τόξο του κύκλου είναι ταχύτερο από οποιοδήποτε αριθμό των χορδών του,
- "Από τα προηγούμενα, είναι δυνατό να συναχθεί ότι ο πιο γρήγορος δρόμος όλων [omnium velocissimam lationem], από ένα σημείο σε ένα άλλο, δεν είναι η συντομότερη διαδρομή, δηλαδή, μια ευθεία γραμμή, αλλά το τόξο του κύκλου.
- ...
- Κατά συνέπεια, όσο περισσότερο το εγγεγραμένο πολύγωνο προσεγγίζει τον κύκλο τόσο συντομότερος είναι ο χρόνος που απαιτείται για την κάθοδο από το Α έως Γ. Αυτό που έχει αποδειχθεί για το τεταρτημόριο ισχύει επίσης και για μικρότερα τόξα. Το σκεπτικό είναι το ίδιο ".
Ο Galileo μελέτησε την κυκλοειδή και της έδωσε το όνομά της, αλλά η σύνδεση μεταξύ αυτής και του προβλήματος του έπρεπε να περιμένει την περαιτέρω πρόοδο στα μαθηματικά. (Από την WIKIPEDIA)
Η λύση του Johan Bernoulli (Από την WIKIPEDIA):
According to Fermat’s principle: The actual path between two points taken by a beam of light is the one which is traversed in the least time. Johann Bernoulli used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).[1]
The conservation law can be used to express the speed of a body in a constant gravitational field as:
 ,
,
Johann Bernoulli noted that the law of refraction gives a constant of the motion for a beam of light in a medium of variable density:
 ,
,
The equations above allow us to draw two conclusions:
- At the onset, when the particle speed is nil, the angle must be nil. Hence, the brachistochrone curve is tangent to the vertical at the origin.
- The speed reaches a maximum value when the trajectory becomes horizontal and the angle θ = 90°.
 .
.
 .
.
Johann's brother Jakob showed how 2nd differentials can be used to obtain the condition for least time. A modernized version of the proof is as follows. If we make a negligible deviation from the path of least time then, for the differential triangle formed by the displacement along the path and the horizontal and vertical displacements,
- ds2 = dx2 + dy2.
 .
.
http://curvebank.calstatela.edu/brach3/brach3.htm
Η (χειρόγραφη) λύση του Newton:
http://www.cosmeo.com/images/pictures/player/BE063184.jpg
Στον παρακάτω σύνδεσμο έχω μια μικρή εργασία για το πως,εφαρμόζοντας τις μεθόδους του λογισμού των μεταβολών(Euler-Lagrange) μπορούμε να αποδείξουμε ότι η συντομότερη γραμμή που συνδέει δύο σημεία (στον Ευκλείδιο χώρο) είναι η ευθεία που περνάει από τα σημεία αυτά.
ΕΥΘΕΙΑ
Και μια πολύ ωραία προσομοίωση για τη βραχιστόχρονη καμπύλη, μέσω του scratch , από το συνάδελφο Νίκο Δαπόντε:
Brachistochrone_Experiment
(Τρέχει απ΄ευθείας στον browser, αλλά χρειάζεται τη java. Πατάμε την πράσινη σημαία για να ξεκινήσει και περιμένουμε λίγο χρόνο για να φτιάξει την κυκλοειδή η γάτα. Μετά πατάμε το start)Τέλος ένα πολύ ενδιαφέρον Site για τη βραχιστόχρονη καμπύλη:
http://curvebank.calstatela.edu/brach/brach.htm
http://curvebank.calstatela.edu/brach2/cucloid2.jpg
http://t2.gstatic.com /images?q=tbn:ANd9GcTnI6ykpUcSVloODQYolsdLUHQwV7oVEk6Roc62C82zaFPIQ6-2



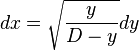








Πολύ ενδιαφέρον θέμα. Μπράβο!
ΑπάντησηΔιαγραφήΜια μικρή αναφορά στο πρόβλημα κάνει και ο David Acheson στο εξαιρετικά διασκεδαστικό του βιβλίο 1089 and all that: A journey into mathematics. Αναφέρει λοιπόν ότι ο μαρκήσιος de l' Hospital έγραψε στον Johann Bernoulli:
ΑπάντησηΔιαγραφήThis problem seems to be one of the most curious and beautiful that has ever been proposed, and I would very much like to apply my efforts to it, but for this it would be necessary that you reduce it to pure mathematics, since physics bothers me... (p. 68)
Η αλήθεια είναι ότι εκείνη την εποχή ο Johann Bernoulli παρέδιδε ιδιαίτερα μαθήματα απειροστικού λογισμού στο μαρκήσιο, έναντι αδράς αμοιβής βέβαια. Επομένως, αυτή η οικειότητα ανάμεσα στους δύο άντρες είναι μάλλον δικαιολογημένη.
Ντίνο, σ΄ευχαριστώ πολύ για το πολύ ενδιαφέρον ιστορικό στοιχείο που μας ανέφερες.
ΑπάντησηΔιαγραφή