Σε τούτη την εξαιρετική συλλογή δοκιμίων ο Poincare ερευνά τα χαρακτηριστικά των μαθηματικών (την ενόραση και τη λογική, τη μέτρηση του χρόνου, την έννοια του χώρου και τις διαστάσεις του) και των φυσικών επιστημών (τη σχέση μεταξύ ανάλυσης και φυσικής, την αστρονομία, την ιστορία και το μέλλον της μαθηματικής φυσικής). Για τον Poincare, σκοπός της επιστήμης δεν είναι η δράση. Η επιστήμη είναι χρήσιμη επειδή είναι αληθινή, αλλά δεν είναι αληθινή επειδή πρόκειται να είναι χρήσιμη. Δεν υπάρχει άλλος σκοπός από αυτή την ίδια, την ανιδιοτελή γνώση, την επιστήμη για την επιστήμη: «Ό,τι ονομάζουμε αντικειμενική πραγματικότητα είναι σε τελευταία ανάλυση αυτό που είναι κοινό για όλα τα σκεπτόμενα όντα, και θα μπορούσε να είναι κοινό για όλους. Αυτό το κοινό στοιχείο δεν μπορεί να είναι παρά η αρμονία που εκφράζεται από τους μαθηματικούς νόμους».
ISBN: 960-7023-96-X
Έτος έκδοσης: 1997
Ξένος εκδότης: Seuil
Πρόλογος βιβλίου: Στέλιος Τσεκούρας
Σελίδες βιβλίου: 208
Εκτύπωση βιβλίου: Α/Μ
Δέσιμο: Χαρτόδετο
Βάρος: 0.33
Διαστάσεις: 14 x 21
Ο Ζυλ Ανρί Πουανκαρέ (γαλλ. Henri Poincaré) ήταν ένας από τους κορυφαίους Γάλλους μαθηματικούς και θεωρητικούς φυσικούς και φιλόσοφους της επιστήμης. Ο Πουανκαρέ γεννήθηκε στις 29 Απριλίου του 1854 και πέθανε στις 17 Ιουλίου του 1912. Συχνά περιγράφεται ως πολυμαθής, και στον κόσμο των μαθηματικών είναι γνωστός ως ο «Τελευταίος Πανεπιστήμονας», καθώς διέπρεπε σε όλα τα επιστημονικά πεδία τα οποία υπήρχαν στη διάρκεια της ζωής του. (Βικιπαίδεια).
Από την WIKIPEDIA:
Jules Henri Poincaré (29 April 1854 – 17 July 1912) (French pronunciation: [ˈʒyl ɑ̃ˈʁi pwɛ̃kaˈʁe]) was a French mathematician, theoretical physicist, engineer, and a philosopher of science. He is often described as a polymath, and in mathematics as The Last Universalist, since he excelled in all fields of the discipline as it existed during his lifetime.
As a mathematician and physicist, he made many original fundamental contributions to pure and applied mathematics, mathematical physics, and celestial mechanics. He was responsible for formulating the Poincaré conjecture, one of the most famous problems in mathematics. In his research on the three-body problem, Poincaré became the first person to discover a chaotic deterministic system which laid the foundations of modern chaos theory. He is also considered to be one of the founders of the field of topology.
Poincaré introduced the modern principle of relativity and was the first to present the Lorentz transformations in their modern symmetrical form. Poincaré discovered the remaining relativistic velocity transformations and recorded them in a letter to Dutch physicist Hendrik Lorentz (1853–1928) in 1905. Thus he obtained perfect invariance of all of Maxwell's equations, an important step in the formulation of the theory of special relativity.
The Poincaré group used in physics and mathematics was named after him.
WORK
Summary
Poincaré made many contributions to different fields of pure and applied mathematics such as: celestial mechanics, fluid mechanics, optics, electricity, telegraphy, capillarity, elasticity, thermodynamics, potential theory, quantum theory, theory of relativity and physical cosmology.He was also a populariser of mathematics and physics and wrote several books for the lay public.
Among the specific topics he contributed to are the following:
- algebraic topology
- the theory of analytic functions of several complex variables
- the theory of abelian functions
- algebraic geometry
- Poincaré was responsible for formulating one of the most famous problems in mathematics, the Poincaré conjecture.
- Poincaré recurrence theorem
- hyperbolic geometry
- number theory
- the three-body problem
- the theory of diophantine equations
- the theory of electromagnetism
- the special theory of relativity
- In an 1894 paper, he introduced the concept of the fundamental group.
- In the field of differential equations Poincaré has given many results that are critical for the qualitative theory of differential equations, for example the Poincaré sphere and the Poincaré map.
- Poincaré on "everybody's belief" in the Normal Law of Errors (see normal distribution for an account of that "law")
- Published an influential paper providing a novel mathematical argument in support of quantum mechanics. ( WIKIPEDIA)
The three-body problem
The problem of finding the general solution to the motion of more than two orbiting bodies in the solar system had eluded mathematicians since Newton's time. This was known originally as the three-body problem and later the n-body problem, where n is any number of more than two orbiting bodies. The n-body solution was considered very important and challenging at the close of the nineteenth century. Indeed in 1887, in honour of his 60th birthday, Oscar II, King of Sweden, advised by Gösta Mittag-Leffler, established a prize for anyone who could find the solution to the problem. The announcement was quite specific:| “ | Given a system of arbitrarily many mass points that attract each according to Newton's law, under the assumption that no two points ever collide, try to find a representation of the coordinates of each point as a series in a variable that is some known function of time and for all of whose values the series converges uniformly. | ” |
Work on relativity
Main articles: Lorentz ether theory and History of special relativity
Local time
Poincaré's work at the Bureau des Longitudes on establishing international time zones led him to consider how clocks at rest on the Earth, which would be moving at different speeds relative to absolute space (or the "luminiferous aether"), could be synchronised. At the same time Dutch theorist Hendrik Lorentz was developing Maxwell's theory into a theory of the motion of charged particles ("electrons" or "ions"), and their interaction with radiation. In 1895 Lorentz had introduced an auxiliary quantity (without physical interpretation) called "local time" and introduced the hypothesis of length contraction to explain the failure of optical and electrical experiments to detect motion relative to the aether (see Michelson–Morley experiment). Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher was interested in the "deeper meaning". Thus he interpreted Lorentz's theory and in so doing he came up with many insights that are now associated with special relativity. In The Measure of Time (1898), Poincaré said, " A little reflection is sufficient to understand that all these affirmations have by themselves no meaning. They can have one only as the result of a convention." He also argued that scientists have to set the constancy of the speed of light as a postulate to give physical theories the simplest form. Based on these assumptions he discussed in 1900 Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronised by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.
and introduced the hypothesis of length contraction to explain the failure of optical and electrical experiments to detect motion relative to the aether (see Michelson–Morley experiment). Poincaré was a constant interpreter (and sometimes friendly critic) of Lorentz's theory. Poincaré as a philosopher was interested in the "deeper meaning". Thus he interpreted Lorentz's theory and in so doing he came up with many insights that are now associated with special relativity. In The Measure of Time (1898), Poincaré said, " A little reflection is sufficient to understand that all these affirmations have by themselves no meaning. They can have one only as the result of a convention." He also argued that scientists have to set the constancy of the speed of light as a postulate to give physical theories the simplest form. Based on these assumptions he discussed in 1900 Lorentz's "wonderful invention" of local time and remarked that it arose when moving clocks are synchronised by exchanging light signals assumed to travel with the same speed in both directions in a moving frame.| Wikisource has original works written by or about: Henri Poincaré |
Principle of relativity and Lorentz transformations
He discussed the "principle of relative motion" in two papers in 1900 and named it the principle of relativity in 1904, according to which no physical experiment can discriminate between a state of uniform motion and a state of rest. In 1905 Poincaré wrote to Lorentz about Lorentz's paper of 1904, which Poincaré described as a "paper of supreme importance." In this letter he pointed out an error Lorentz had made when he had applied his transformation to one of Maxwell's equations, that for charge-occupied space, and also questioned the time dilation factor given by Lorentz. In a second letter to Lorentz, Poincaré gave his own reason why Lorentz's time dilation factor was indeed correct after all: it was necessary to make the Lorentz transformation form a group and gave what is now known as the relativistic velocity-addition law. Poincaré later delivered a paper at the meeting of the Academy of Sciences in Paris on 5 June 1905 in which these issues were addressed. In the published version of that he wrote:| “ | The essential point, established by Lorentz, is that the equations of the electromagnetic field are not altered by a certain transformation (which I will call by the name of Lorentz) of the form: | ” |

and showed that the arbitrary function
 must be unity for all
must be unity for all  (Lorentz had set
(Lorentz had set 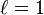 by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination x2 + y2 + z2 − c2t2 is invariant. He noted that a Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing
by a different argument) to make the transformations form a group. In an enlarged version of the paper that appeared in 1906 Poincaré pointed out that the combination x2 + y2 + z2 − c2t2 is invariant. He noted that a Lorentz transformation is merely a rotation in four-dimensional space about the origin by introducing 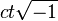 as a fourth imaginary coordinate, and he used an early form of four-vectors. Poincaré’s attempt at a four-dimensional reformulation of the new mechanics was rejected by himself in 1907, because in his opinion the translation of physics into the language of four-dimensional geometry would entail too much effort for limited profit. So it was Hermann Minkowski who worked out the consequences of this notion in 1907. ( WIKIPEDIA )
as a fourth imaginary coordinate, and he used an early form of four-vectors. Poincaré’s attempt at a four-dimensional reformulation of the new mechanics was rejected by himself in 1907, because in his opinion the translation of physics into the language of four-dimensional geometry would entail too much effort for limited profit. So it was Hermann Minkowski who worked out the consequences of this notion in 1907. ( WIKIPEDIA )Mass–energy relation
Like others before, Poincaré (1900) discovered a relation between mass and electromagnetic energy. While studying the conflict between the action/reaction principle and Lorentz ether theory, he tried to determine whether the center of gravity still moves with a uniform velocity when electromagnetic fields are included. He noticed that the action/reaction principle does not hold for matter alone, but that the electromagnetic field has its own momentum. Poincaré concluded that the electromagnetic field energy of an electromagnetic wave behaves like a fictitious fluid ("fluide fictif") with a mass density of E/c2. If the center of mass frame is defined by both the mass of matter and the mass of the fictitious fluid, and if the fictitious fluid is indestructible — it's neither created or destroyed — then the motion of the center of mass frame remains uniform. But electromagnetic energy can be converted into other forms of energy. So Poincaré assumed that there exists a non-electric energy fluid at each point of space, into which electromagnetic energy can be transformed and which also carries a mass proportional to the energy. In this way, the motion of the center of mass remains uniform. Poincaré said that one should not be too surprised by these assumptions, since they are only mathematical fictions.However, Poincaré's resolution led to a paradox when changing frames: if a Hertzian oscillator radiates in a certain direction, it will suffer a recoil from the inertia of the fictitious fluid. Poincaré performed a Lorentz boost (to order v/c) to the frame of the moving source. He noted that energy conservation holds in both frames, but that the law of conservation of momentum is violated. This would allow perpetual motion, a notion which he abhorred. The laws of nature would have to be different in the frames of reference, and the relativity principle would not hold. Therefore he argued that also in this case there has to be another compensating mechanism in the ether.
Poincaré himself came back to this topic in his St. Louis lecture (1904). This time (and later also in 1908) he rejected the possibility that energy carries mass and criticized the ether solution to compensate the above mentioned problems:
| “ | The apparatus will recoil as if it were a cannon and the projected energy a ball, and that contradicts the principle of Newton, since our present projectile has no mass; it is not matter, it is energy. [..] Shall we say that the space which separates the oscillator from the receiver and which the disturbance must traverse in passing from one to the other, is not empty, but is filled not only with ether, but with air, or even in inter-planetary space with some subtile, yet ponderable fluid; that this matter receives the shock, as does the receiver, at the moment the energy reaches it, and recoils, when the disturbance leaves it? That would save Newton's principle, but it is not true. If the energy during its propagation remained always attached to some material substratum, this matter would carry the light along with it and Fizeau has shown, at least for the air, that there is nothing of the kind. Michelson and Morley have since confirmed this. We might also suppose that the motions of matter proper were exactly compensated by those of the ether; but that would lead us to the same considerations as those made a moment ago. The principle, if thus interpreted, could explain anything, since whatever the visible motions we could imagine hypothetical motions to compensate them. But if it can explain anything, it will allow us to foretell nothing; it will not allow us to choose between the various possible hypotheses, since it explains everything in advance. It therefore becomes useless. | ” |
It was Albert Einstein's concept of mass–energy equivalence (1905) that a body losing energy as radiation or heat was losing mass of amount m = E/c2 that resolved Poincaré's paradox, without using any compensating mechanism within the ether. The Hertzian oscillator loses mass in the emission process, and momentum is conserved in any frame. However, concerning Poincaré's solution of the Center of Gravity problem, Einstein noted that Poincaré's formulation and his own from 1906 were mathematically equivalent. ( WIKIPEDIA )
Poincaré and Einstein
Einstein's first paper on relativity was published three months after Poincaré's short paper, but before Poincaré's longer version. It relied on the principle of relativity to derive the Lorentz transformations and used a similar clock synchronisation procedure (Einstein synchronisation) that Poincaré (1900) had described, but was remarkable in that it contained no references at all. Poincaré never acknowledged Einstein's work on special relativity. Einstein acknowledged Poincaré in the text of a lecture in 1921 called Geometrie und Erfahrung in connection with non-Euclidean geometry, but not in connection with special relativity. A few years before his death Einstein commented on Poincaré as being one of the pioneers of relativity, saying "Lorentz had already recognised that the transformation named after him is essential for the analysis of Maxwell's equations, and Poincaré deepened this insight still further ...." ( WIKIPEDIA )(Για την Επιστημονική Δημιουργία):
Αποδεικνύουμε με τη λογική, επινοούμε με τη διαίσθηση.
Η λογική παραμένει στείρα, εκτός εάν γονιμοποιηθεί από τη διαίσθηση.
Η εμπειρία είναι η αποκλειστική πηγή όλης της αλήθειας.
Η επιστήμη είναι δεδομένα.
Ακριβώς όπως τα σπίτια χτίζονται με τούβλα,
έτσι και η επιστήμη χτίζεται με δεδομένα.
Αλλά όπως ένας σωρός τούβλα δεν κάνει ένα σπίτι,
έτσι και μια συλλογή δεδομένων δεν είναι απαραίτητα επιστήμη.
Να αμφιβάλεις για τα πάντα και να πιστεύεις σε όλα
είναι και οι δυο πολύ άνετες στάσεις, γιατί και οι δυο
απελευθερώνουν από την ανάγκη να σκέφτεσαι...
Απλά να συμπληρώσω ότι το όνομα του συγγραφέα αποτελεί εγγύηση για την αξία του συγκεκριμένου βιβλίου και το όνομα του μεταφραστή για την σωστή και ευανάγνωστη απόδοσή του στη γλώσσα μας.
H προσωπική ιστοσελίδα του Στέλιου Τσεκούρα:
Η αναφορά του Ανδρέα Κασσέτα στον Poincare:
| (ΕΔΩ) |




Μας βάζεις πολύ διάβασμα για το καλοκαίρι Γιάννη. Παρουσιάζεις τόσο ελκυστικά τα θέματα σου που δεν ξέρω τι να πρωτοαγοράσω!
ΑπάντησηΔιαγραφή