Το Πρόβλημα της Βραχιστόχρονης καμπύλης (II) . Mια πλήρης μελέτη από το συνάδελφο Βαγγέλη Κορφιάτη.

    (Ευχαριστώ το συνάδελφο Γιάννη Καλατζή για την ορθογραφική και συντακτική διόρθωση στον τίτλο της ανάρτησης)        

       Καταχωρώντας την ανάρτηση : "Το πρόβλημα του βραχιστόχρονης καμπύλης" στο δίκτυο: "Υλικό Φυσικής Χημείας" στο οποίο είμαι μέλος, ανάμεσα στα άλλα σχόλια υπήρξε και μία απάντηση από το συνάδελφο Βαγγέλη Κορφιάτη, η οποία στην ουσία ήταν μια ολοκληρωμένη μελέτη του προβλήματος. Στη εργασία του λοιπόν αυτή ο συνάδελφος, παράγει:

• Τις εξισώσεις της κυκλοειδούς καμπύλης
• Την διατύπωση του προβλήματος της βραχιστόχρονης καμπύλης.
• Τις εξισώσεις Euler – Lagrange
• Την επίλυση του προβλήματος.

Μάλιστα δε, επιλέγει και συγκρίνει (καταλήγοντας σε συγκεκριμμένα αριθμητικά αποτελέσματα) τον χρόνο καθόδου στην περίπτωση ευθύγραμμου τμήματος, τεταρτοκυκλίου και κυκλοειδούς καμπύλης.

Η ΒΡΑΧΙΣΤΟΧΡΟΝΗ ΚΑΜΠΥΛΗ ΚΑΙ ΟΙ ΕΞΙΣΩΣΕΙΣ EULER - LAGRANGE

( Βαγγέλης Κορφιάτης, PhD) 

 

 

                                               

Η σταθερότητα των ατόμων (ανανεωμένο). (N. Bohr)

   ... Εφ’ όσον το ηλεκτρόνιο περιστρέφεται γύρω από τον πυρήνα σε κυκλική τροχιά έχει κεντρομόλο επιτάχυνση και άρα σύμφωνα με την ηλεκτρομαγνητική θεωρία του Maxwell πρέπει να εκπέμπει ηλεκτρομαγνητική ακτινοβολία. Επομένως (Διατήρηση της Ενέργειας ) θα πρέπει να χάνει συνεχώς ενέργεια κάτι που θα’ χει σαν συνέπεια να κινείται σε σπειροειδή τροχιά με διαρκώς μειούμενη ακτίνα και διαρκώς μεταβαλλόμενη συχνότητα ,μέχρις ότου να πέσει τελικά στον πυρήνα. Μάλιστα μια εκτίμηση της τάξης μεγέθους δείχνει ότι ο χρόνος πτώσης του ηλεκτρονίου στον πυρήνα είναι της τάξης του 0,0000000001 s.  Έτσι, σύμφωνα με την κλασική θεωρία το άτομο αποδεικνύεται ένα εξαιρετικά βραχύβιο κατασκεύασμα, που όμως δεν είναι.

     https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhaIs2ez8C5gN0HGV_J7KYZmhh_xfd84Xz7Jgy9ODpCEW7rIufnGYJzEO6Sf3RIqZALjOE5npAIOd3dbG8NgCgOblqtU8U7muM4FtvhtSZ4ZYCX2JaMMQNhMC6pLohQeZNk1Hk7cAu0W1D3/s1600/Maxwell.jpg

     Από την άλλη πλευρά καθώς το ηλεκτρόνιο εκτελεί απεριοδική κίνηση κατά την σπειροειδή περιστροφή του γύρω απ’ τον πυρήνα θάπρεπε να εκπέμπει συνεχές και όχι γραμμικό φάσμα. Είναι γνωστό όμως ότι τα αέρια εκπέμπουν γραμμικά φάσματα.

    Και βέβαια το κλασικό μοντέλο αδυνατεί να εξηγήσει τη σταθερότητα των ατόμων. Τα άτομα π.χ. ενός αερίου βρίσκονται σε μια αδιάκοπη θερμική κίνηση , με εκατομμύρια αμοιβαίες κρούσεις το δευτερόλεπτο και με ταχύτητες της τάξης των δεκάδων χιλιάδων μέτρων ανά δευτερόλεπτο . Και όμως αναδύονται από τις αμοιβαίες αυτές κρούσεις τους  τελείως αμετάβλητα. Αυτό δεν θα είχαμε καμιά δυσκολία να το αντιληφθούμε αν τα άτομα ήταν πραγματικά ά-τομα και άρα «εξαιρετέα από την αλλαγή και την φθορά » όπως λέει ο Επίκουρος. Αλλά δεν είναι. Τα άτομα διασπώνται και ανασυντίθενται , καταστρέφονται και αναδημιουργούνται .   Συμμετέχουν σε χημικές αντιδράσεις. Και πάντοτε ξαναβγαίνουν τα ίδια . Σαν να μην έχουν ιστορία και προϊστορία . Σαν η μορφή τους να είναι προκαθορισμένη . ...    

                           http://www.glogster.com/media/5/35/29/25/35292540.jpg

  http://nothingnerdy.wikispaces.com/file/view/bohr_hydrogen.gif/88059503/bohr_hydrogen.gif



Μπορείτε να κατεβάσετε την μικρή εργασία για τη σταθερότητα των ατόμων................................................................................ΕΔΩ

Το Πρόβλημα της Βραχιστόχρονης καμπύλης. The Brachistochrone Problem . (Johann Bernoulli, Isaac Newton, Jakob Bernoulli , Gottfried Leibniz , Ehrenfried Walther von Tschirnhaus, Guillaume de l'Hopital).

(Ευχαριστώ το συνάδελφο Γιάννη Καλατζή για την ορθογραφική και συντακτική διόρθωση στον τίτλο της ανάρτησης)

                                                      Johan Bernoulli
                  http://www.librosmaravillosos.com/matematicalife/imagenes/113a.gif

          http://online.redwoods.cc.ca.us/instruct/darnold/calcproj/fall98/nateb/iv14m.gif

             Ο Johann Bernoulli έθεσε το πρόβλημα της βραχιστόχρονης  (brachistochrone) καμπύλης προς τους αναγνώστες του Acta Eruditorum τον Ιούνιο, 1696.  Δημοσίευσε τη λύση του στο περιοδικό τον  Μάιο του επόμενου έτους, και υπογράμμισε ότι η λύση είναι η ίδια καμπύλη με την ταυτόχρονη ( tautochrone) καμπύλη του Huygens . Πέντε μαθηματικοί απάντησαν με λύσεις: ο Ισαάκ Νεύτων , ο Jakob Bernoulli (αδελφός του Johann), ο Gottfried Leibniz ,  ο Ehrenfried Walther von Tschirnhaus και ο Guillaume de l'Hopital . Τέσσερις από τις λύσεις (εκτός αυτής του de l'Hôpital) δημοσιεύθηκαν στην ίδια έκδοση του περιοδικού, μαζί με αυτή του Johann Bernoulli . 

          Σε μια προσπάθεια να ξεπεράσει τον αδελφό του, Jacob Bernoulli  ο Johan δημιούργησε μια σκληρότερη εκδοχή του brachistochrone προβλήματος. Στην προσπάθεια επίλυσής του, ανέπτυξε νέες μεθόδους που τελειοποιήθηκαν αργότερα από τον Λέοναρντ Όιλερ σε αυτό που ονομάζουμε  λογισμό των μεταβολών .Ο  Joseph-Louis de Lagrange συνέχισε τις έρευνες  που τελικά οδήγησαν  σε μια σύγχρονη εκδοχή του απειροστικού λογισμού .

          Ο Γαλιλαίος επιχείρησε να λύσει ένα παρόμοιο πρόβλημα για την πορεία της ταχύτερης καθόδου από ένα σημείο σε ένα τοίχο στο έργο του δύο νέες επιστήμες το 1638. Κατέληξε στο συμπέρασμα  ότι το τόξο του κύκλου είναι ταχύτερο από οποιοδήποτε αριθμό των χορδών του,

"Από τα προηγούμενα, είναι δυνατό να συναχθεί ότι ο πιο γρήγορος δρόμος όλων [omnium velocissimam lationem], από ένα σημείο σε ένα άλλο, δεν είναι η συντομότερη διαδρομή, δηλαδή, μια ευθεία γραμμή, αλλά το τόξο του κύκλου.

...

Κατά συνέπεια, όσο περισσότερο το εγγεγραμένο πολύγωνο προσεγγίζει τον  κύκλο τόσο συντομότερος  είναι ο χρόνος που απαιτείται για την κάθοδο από το Α έως Γ. Αυτό που  έχει αποδειχθεί για το τεταρτημόριο  ισχύει επίσης και για μικρότερα τόξα.  Το σκεπτικό είναι το ίδιο ".

        Ο  Galileo μελέτησε την κυκλοειδή  και της έδωσε το όνομά της, αλλά η σύνδεση μεταξύ αυτής και του προβλήματος του έπρεπε να περιμένει την περαιτέρω πρόοδο στα μαθηματικά.  (Από την WIKIPEDIA)

Η λύση του Johan Bernoulli (Από την WIKIPEDIA):

According to Fermat’s principle: The actual path between two points taken by a beam of light is the one which is traversed in the least time. Johann Bernoulli used this principle to derive the brachistochrone curve by considering the trajectory of a beam of light in a medium where the speed of light increases following a constant vertical acceleration (that of gravity g).^[1]
The conservation law can be used to express the speed of a body in a constant gravitational field as:

,

where y represents the vertical distance the body has fallen. By conservation of energy the speed of motion of the body along an arbitrary curve does not depend on the horizontal displacement.
Johann Bernoulli noted that the law of refraction gives a constant of the motion for a beam of light in a medium of variable density:

,

where v_m is the constant and θ represents the angle of the trajectory with respect to the vertical.
The equations above allow us to draw two conclusions:

1. At the onset, when the particle speed is nil, the angle must be nil. Hence, the brachistochrone curve is tangent to the vertical at the origin.
2. The speed reaches a maximum value when the trajectory becomes horizontal and the angle θ = 90°.

To keep things simple we can assume that the particle (or the beam) with coordinates (x,y) departs from the point (0,0) and reaches maximum speed after a falling a vertical distance D. So,

.

Rearranging terms in the law of refraction and squaring gives:

which can be solved for dx in terms of dy:

.

Substituting from the expressions for v and v_m above gives:

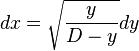
which is the differential equation of an inverted cycloid generated by a circle of diameter D.
Johann's brother Jakob showed how 2nd differentials can be used to obtain the condition for least time. A modernized version of the proof is as follows. If we make a negligible deviation from the path of least time then, for the differential triangle formed by the displacement along the path and the horizontal and vertical displacements,

ds² = dx² + dy².

On differentiation with dy fixed we get,

.

And finally rearranging terms gives,

where the last part is just the change in distance for given change in time for 2nd differentials. Now consider the changes along the two neighboring paths in the figure below for which the horizontal separation between paths along the central line is d²x (the same for both the upper and lower differential triangles). Along the old and new paths, the parts that differ are,

For the path of least times these times are equal so for their difference we get,

And the condition for least time is,

                                     http://curvebank.calstatela.edu/brach3/brach3.htm

 Η (χειρόγραφη) λύση του Newton:

                                  http://www.cosmeo.com/images/pictures/player/BE063184.jpg 


   
             Στον παρακάτω σύνδεσμο έχω μια μικρή εργασία για το πως,εφαρμόζοντας τις μεθόδους του λογισμού των μεταβολών(Euler-Lagrange) μπορούμε να αποδείξουμε ότι η συντομότερη γραμμή που συνδέει δύο σημεία (στον Ευκλείδιο χώρο) είναι η ευθεία που περνάει από τα σημεία αυτά.

ΕΥΘΕΙΑ



Και μια πολύ ωραία προσομοίωση για τη βραχιστόχρονη καμπύλη, μέσω του scratch , από το συνάδελφο Νίκο Δαπόντε:

Brachistochrone_Experiment

(Τρέχει απ΄ευθείας στον browser, αλλά χρειάζεται τη java. Πατάμε την πράσινη σημαία για να ξεκινήσει και περιμένουμε λίγο χρόνο για να φτιάξει την κυκλοειδή η γάτα. Μετά πατάμε το start)


     Τέλος ένα πολύ ενδιαφέρον Site για τη βραχιστόχρονη καμπύλη:

http://curvebank.calstatela.edu/brach/brach.htm

                               http://curvebank.calstatela.edu/brach2/cucloid2.jpg

              http://t2.gstatic.com /images?q=tbn:ANd9GcTnI6ykpUcSVloODQYolsdLUHQwV7oVEk6Roc62C82zaFPIQ6-2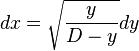